 |
 |
|
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1983 >> Районный тур >> 8 класс | Показать решения |
|
|
| Санкт-Петербургская (Ленинградская) математическая олимпиада. 1983. Районный тур. 8 класс |
|
|
Задача 1:
Найти значение дроби  ,
если
,
если 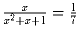 .
.
Задача 2:
Задача 3: На одной стороне угла с вершиной O отложены равные отрезки OA = AB = BC, на другой стороне – равные отрезки OD = DE = EF. Докажите, что треугольники AEC и DBF равновелики.
Задача 4: Число членов арифметической прогрессии, разность которой отлична от нуля, четно, но не кратно 4. Сумма членов с четными номерами противоположна сумме членов с нечетными номерами. Докажите, что произведение всех членов прогрессии отрицательно.
Задача 5: Докажите, что для углов произвольного треугольника ABC справедливо равенство: sin ²A = sin ²B + sin ²C – 2 sin B sin C cos A.
| Задачная база >> Санкт-Петербургские (Ленинградские) соревнования >> Городская олимпиада >> 1983 >> Районный тур >> 8 класс | Показать решения |