 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1994 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1994 |
|
|
Сосчитайте сумму:
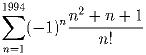
Задача 2:
Докажите, что каждая натуральная степень числа 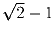 может
быть записана в виде
может
быть записана в виде 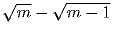 , где m – некоторое целое
число (например
, где m – некоторое целое
число (например 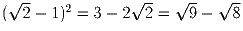 ).
).
Задача 3:
За круглым столом сидит 25 человек. Каждый час проходит голосование и каждый должен сказать «да» или «нет». Каждый из 25 голосующих придерживается следующего правила: если во время n-ого голосовани его ответ совпадает с ответом одного из его соседей, то во врем следующего голосования его мнение не меняется, а если его мнение расходится с мнением обоих соседей, то в следующий раз этот человек меняет свой ответ на противоположный. Докажите, что вне зависимости от того как будут распределены голоса во время первого голосования, настанет такой момент времени, когда все перестанут менять свои ответы.
Задача 4:
AB – диаметр окружности. Через точку P, не лежащую на прямой AB провели прямые AP и PB, которые пересекают окружность в точках U и V соответственно. |PU| = s|PA|, |PV| = t|PB|. Выразите cos ∠ APB через s и t.
Задача 5:
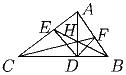
ABC – остроугольный треугольник. AD – высота, опущенная на сторону BC, H – произвольная точка на отрезке AD, отличная от его концов. Прямые BH и CH пересекают стороны AC и BC в точках E и F соответственно. Докажите, что ∠ EDH = ∠ FDH.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1994 | Показать решения |