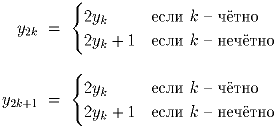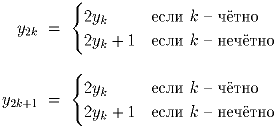Задача 1: Рассмотрим треугольник, у которого все три стороны и высота – последовательные натуральные числа, причём высота делит треугольник на два прямоугольных треугольника с целыми сторонами. Докажите, что такой треугольник ровно один.

Задача 2: Докажите, что число x рационально в том и только том случае, если в последовательности x, x + 1, x + 2, x + 3,  …  найдутся три элемента, образующие геометрическую прогрессию.

Задача 3: В треугольнике ABC медианы к сторонам AB и AC перпендикулярны. Докажите, что  ctg B +  ctg C ≥ ⅔.

Задача 4: В теннисном турнире участвовали ученики нескольких школ. Никакие два участника одной школы не играли друг с другом. Любые два участника из разных школ играли друг с другом ровно один матч. Общее количество мальчиков отличается от общего количества девочек не более чем на 1. Общее количество матчей между двумя мальчиками или двумя девочками отличалось от количества матчей между мальчиком и девочкой не более чем на 1. Какое максимальное количество школ могло быть представлено нечётным числом участников?

Задача 5: Пусть y₁, y₂, y₃,… – такая последовательность, что y₁ = 1 и, для k > 0 выполнены следующие равенства: