 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1990 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1990 |
|
|
Соревнование, в котором принимали участие n ≥ 2 игроков, длилось k дней. Каждый день каждый игрок получал от 1 до n очков, причём все результаты были различны. По окончании соревнования оказалось, что все игроки получили по 26 очков. Найдите все пары (n,k) для которых такое возможно.
Задача 2: ½n(n + 1) различных натуральных чисел расположены в случайном порядке в треугольной таблице:

Пусть Mk – максимальное число в k-й строке сверху. Найдите вероятность того, что M1 < M2 < M3 … < Mn
Задача 3: Пусть ABCD – выпуклый вписанный четырёхугольник, и пусть диагонали AC и BD пересекаются в точке X. Из точки X опущены перпендикуляры XA′, XB′, XC′ и XD′ на стороны AB, BC, CD и DA соответственно. Докажите, что |A′B′| + |C′D′| = |A′D′| + |B′C′|. (|A′B′| – длина отрезка A′B′, и т.д.) Задача 4: Частица может передвигаться со скоростью до 2 метров в секунду вдоль оси абсцисс и со скоростью до 1 метра в секунду в любом другом месте плоскости. Постройте эскиз области, которой может достичь частица, начинающая свой путь в начале координат.Задача 5: Функция f, определённая на множестве натуральных чисел, удовлетворяет следующим условиям:
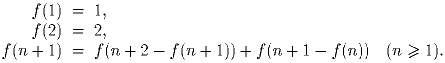
(i) 0 ≤ f(n + 1) – f(n) ≤ 1;
(ii) если значение f(n) нечётно, то f(n + 1) = f(n) + 1.
(b) Определите все значения n для которых f(n) = 2¹º + 1.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1990 | Показать решения |