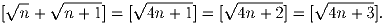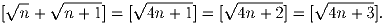Задача 1:

Найдите все натуралные решения уравнения a² + b² = n! с a ≤ b и n < 14.

Задача 2:

В системе счисления с основанием b число 1987 трехзначно и записывается xyz. Найдите x,y,z и b, если x + y + z = 1 + 9 + 8 + 7.

Задача 3:

На стороне BC параллелограмма ABCD взяли точку E. Треугольники DEC, BED и BAD – равнобедренные, чему может быть равен угол DAB?

Задача 4:

На плоскости стоит n человек, все попарные расстояния между которыми различны. Каждый из них обливает водой того, кто стоит ближе всего к нему. Докажите, чтио если n нечетно, то по крайней мере один человек останется сухим. Верно ли это, если n четно?

Задача 5:

Докажите, что для любого натурального n