 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1985 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1985 |
|
|
Стороны треугольника равны 6, 8 и 10. Докажите, что существует единственная прямая, которая делит пополам одновременно площадь и периметр.
Задача 2:
Верно ли, что существует натуральное число, которое удваивается при переносе его первой цифры в конец?
Задача 3:
P1 и P2 – правильные 1985-угольники периметров x1 и x2. P1 – вписан, а P2 – описан вокруг окружности длины c. Докажите, что x + y ≥ 2c
Задача 4:
Докажите, что 2n – 1 делит n! тогда и только тогда, когда n – степень двойки.
Задача 5:
1 < x1 < 2, 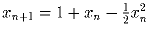 . Докажите, что
. Докажите, что
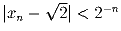 при n ≥ 3.
при n ≥ 3.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1985 | Показать решения |