 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1979 | Показать решения |
|
|
| Канадская математическая олимпиада.. 1979 |
|
|
a и b – положительные числа, a,A1,A2,b – арифметическа прогрессия, a,G1,G2,b – геометрическая прогрессия. Докажите, что A1A2 ≥ G1G2.
Задача 2:
Докажите, что сумма всех двугранных углов тетраэдра не постоянна (в отличие от суммы углов треугольника).
Задача 3:
a,b,c,d,e – целые числа, притом 1 ≤ a < b < c < d < e. Докажите, что
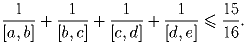
Задача 4:
Волк, сидящий в центре круглой клетки замечает зайца у края и начинает за ним гнаться. Заяц убегает с постоянной скоростью вдоль края клетки, волк догоняет зайца с той же скоростью при этом в любой момент времени находится на отрезке, соединяющем зайца с центром круга. Докажите, что волк догонит зайца в тот момент, когда заяц пробежит четверть круга.
Задача 5:
f(n) – количество самонепересекающихся путей длины n выходящих из начала координат клетчатой плоскости и идущих вдоль линий сетки. Вычислите f(1),f(2),f(3),f(4), и докажите, что 2n < f(n) ≤ 4 • 3n – 1.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1979 | Показать решения |