Задача 1:

Задача 2:

Задача 3: Докажите неравенство:

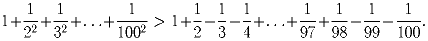
Решение: Разобьем левую и правую части неравенства на группы из четырех слагаемых и докажем, что сумма чисел в группе левой части больше, чем сумма чисел в соответствующей группе правой части, то есть

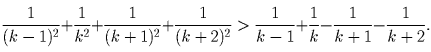
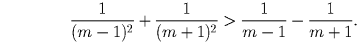
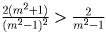Чтобы доказать это, достаточно проверить, что

Это неравенство равносильно такому: , что эквивалентно очевидному неравенству m² + 1 > m² – 1. Что и требовалось.

Задача 4: В выпуклом четырехугольнике две противоположные стороны равны, а произведение синусов углов, прилежащих к одной из равных сторон, равно произведению синусов углов, прилежащих к другой. Докажите, что четырехугольник является параллелограммом или равнобедренной трапецией.

Решение:

Пусть AB и CD – равные стороны четырёхугольника ABCD. Обозначив его углы через  α , β , γ , δ , запишем условие:  sin  α  •  sin  β  =  sin  γ  •  sin  δ . Воспользуемся выражением произведения синусов через косинусы:  cos ( α  –  β ) –  cos ( α  +  β ) =  cos ( γ  –  δ ) –  cos ( γ  +  δ ).

Поскольку  α  +  β  = 360 – ( γ  +  δ ), равенство можно переписать в виде  cos ( α  –  β ) =  cos ( γ  –  δ ), Откуда  α  –  β  =  γ  –  δ  или  α  –  β  =  δ  –  γ . В первом случае  α  +  δ  =  β  +  γ , и четырёхугольник ABCD является параллелограммом. Во втором случае  α  +  γ  =  β  +  δ , то есть ABCD – вписанный четырёхугольник. А вписанный четырёхугольник с двумя равными сторонами является равнобедренной трапецией.

Задача 5: