Задача 1:

Найдите все вещественные решения уравнения [a/2] + [a/3] + [a/5] = a.

Задача 2:

Найдите все вещественные x, которые удовлетворяют равенству x = (x – 1/x)^1/2 + (1 – 1/x)^1/2.

Задача 3:

Докажите, что для всех n ≥ 2

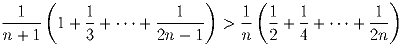
Задача 4:

В треугольнике ABC  ∠ BAC = 40 и  ∠ ABC = 60. На сторонах AC и AB взяли точки D и E соответственно, такие, что  ∠ CBD = 40 и  ∠ BCE = 70. F – точка пересечения BD и CE. Докажите, что AF и BC перпендикулярны.

Задача 5:

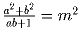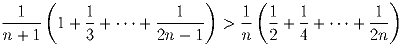
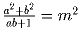Последовательность a_n задана соотношениями: a₀ = 0,a₁ = m, a_n + 1 = m²a_n – a_n – 1. Докажите, все целочисленные решения уравнения с a < b совпадают с парами (a_n,a_n + 1).