 |
 |
|
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1978 | Убрать решения |
|
|
| Канадская математическая олимпиада.. 1978 |
|
|
На какую цифру оканчивается квадрат натурального числа, если в разряде десятков квадрата стоит цифра 7?
Решение:
Запишем число в виде 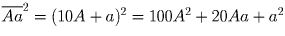 . Заметим,
что четность цифры десятков определяется четностью десятков a².
Следовательно a = 4 или a = 6. В обоих случаях последняя цифра
квадрата равна 6.
. Заметим,
что четность цифры десятков определяется четностью десятков a².
Следовательно a = 4 или a = 6. В обоих случаях последняя цифра
квадрата равна 6.
Задача 2:
Найдите все пары натуральных чисел a,b, удовлетворяющих уравнению 2a² = 3b³.
Решение:
Пусть a = 2n3mx, b = 2k3ly. Тогда 2n + 1 = 3k, 2m = 3l + 1 и x² = y³. Получаем, что k и l – произвольные нечетные числа, следовательно, n = 3t + 1, k = 2t + 1, l = 2s + 1, m = 3s + 2. Очевидно, что x = p³, y = p². Таким образом a = 23t + 133s + 2p³, b = 22t + 132s + 1p².
Задача 3:
Найдите наибольшее вещественное z такое, что при некоторых вещественных x и y
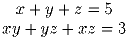
Решение:
Заметим, что x,y и z являются корнями многочлена
P(t) = t³ – 5t² + 3t + a. Изменение параметра a соответствует сдвигу
графика P вдоль оси ординат. При сдвиге графика вниз значение
максимального корня многочлена увеличивается. Заметим, что многочлен
должен иметь 3 вещественных корня, следовательно, максимальное
значение z достигается в том случае, когда P имеет кратный корень
x = y (максимально «низкое» положение графика, при котором есть 3
корня). Откуда 2x + z = 5, x² + 2xz – 3 = 0. Откуда x1 = 3,z1 = – 1, 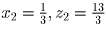 . Следовательно, максимальное значение
. Следовательно, максимальное значение
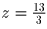 .
.
Задача 4:
Продолжения сторон AD и BC выпуклого четырехугольника ABCD пересекаются в точке E. H и G – середины BD и AC соответственно. Найдите отношение площадей треугольника EHG и четырехугольника ABCD.
Решение:
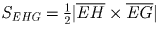 (
(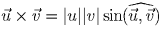 –
псевдовекторное произведение).
–
псевдовекторное произведение).
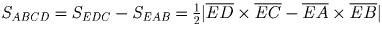 . Поскольку
. Поскольку
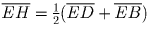 и
и
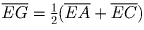 , то
, то
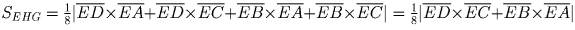 Следовательно (поскольку
Следовательно (поскольку 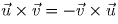 )
SEHG:SABCD = 1:4.
)
SEHG:SABCD = 1:4.
Задача 5:
Eve и Odette играют в следующую игру на доске 3 × 3: за свой ход игрок может поставить на любое свободное поле доски либо черную, либо белую шашку. В конце игры Eve получает по очку за каждую строчку, столбец, или диагональ, в которой нечетное количество черных шашек, Odette – за каждую строчку, столбец или диагональ с четным количеством черных шашек. Выигрывает тот, кто получит больше очков. a) Возможна ли ничья в этой игре? b) Опишите выигрышную стратегию дл первого игрока.
Задача 6:
Нарисуйте график x³ + xy + y³ = 3.
| Задачная база >> Национальные зарубежные олимпиады >> Канада >> 1978 | Убрать решения |