 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Делимость, остатки (профи) | Убрать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Делимость, остатки (профи) |
|
|
Задача 1: Пусть a – целое, b – натуральное число. Тогдаa можно единственным образом представить в виде a = kb + r, где k и r – целые, 0 ≤ r < b.
Задача 2:
x = 100k – 16, k – целое. Чему равны частное и остаток при делении x а) на 100; б) на 5?
Задача 3: Делимое и делитель увеличили в три раза. Как изменятся неполное частное и остаток?
Задача 4: Разность двух чисел делится на b. Докажите, что числа дают одинаковые остатки при делении на b.
Задача 5: Докажите, что остаток от деления простого числа на 30 – простое число или 1.
Задача 6: Пусть число a1 дает при делении на b остаток r1, число a2 – остаток r2. Тогда
а) (сложение остатков) Число a1+a2 при делении на b дает тот же остаток, что и число r1 + r2.
б) (вычитание остатков) Число a1 – a2 при делении на b дает тот же остаток, что и число r1 – r2.
в) (умножение остатков) Число a1a2 при делении на b дает тот же остаток, что и число r1r2.
Задача 7: Докажите, что натуральное число сравнимо а) со своей суммой цифр по модулю 9; б) со своей знакочередующейся суммой цифр по модулю 11.
Задача 8: Докажите, что делится на 24 а) произведение 4 последовательных целых чисел; б) разность квадратов двух простых чисел, больших 3.
Задача 9:
(правило сокращения)
Пусть m и b – взаимно просты. Тогда 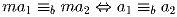 .
.
Задача 10: Найдите все такие x, что 19x оканчивается на 99.
Задача 11: В прямоугольном треугольнике все стороны целые. Докажите, что его площадь делится на 6.
Задача 12: Можно ли клетчатый квадрат 1999 × 1999 разрезать по границам клеток на 10000 прямоугольников с равными диагоналями?
Задача 13: Может ли сумма 13 точных квадратов быть точным квадратом?
Задача 14: Пусть m не делится на простое число p. Тогда
(малая теорема Ферма)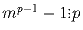 .
.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Делимость, остатки (профи) | Убрать решения |